Perform full SCA analysis on the S1A serine protease dataset

This example shows the full process to perform a complete SCA analysis and detect eXtremal Co-evolving Residues (XCoR) from data importation and MSA filtering to the computation of a SCA coevolution matrix, the extraction of principal and independent components, and the representation of coevolution within and between XCoRs.

Finally, we export fasta files that are necessary for the XCoR visualization along a phylogenetic tree.

# Author: Margaux Jullien <margaux.jullien@univ-grenoble-alpes.fr>
#         Nelle Varoquaux <nelle.varoquaux@univ-grenoble-alpes.fr>
#         Ivan Junier <ivan.junier@univ-grenoble-alpes.fr>
# License: TBD

Import necessary

import cocoatree.datasets as c_data
import cocoatree.io as c_io
import cocoatree.msa as c_msa
import cocoatree.statistics.position as c_pos
import cocoatree.statistics.pairwise as c_pw
import cocoatree.deconvolution as c_deconv

import matplotlib.pyplot as plt
import numpy as np

Load the dataset

We start by importing the dataset. In this case, we can directly load the S1 serine protease dataset provided in cocoatree. To work on your own dataset, you can use cocoatree.io.load_MSA().

A detailed description of how to access all the objects included in the dataset is available here: S1A serine proteases

serine_dataset = c_data.load_S1A_serine_proteases('rivoire')
loaded_seqs = serine_dataset["alignment"]
loaded_seqs_id = serine_dataset["sequence_ids"]
n_loaded_pos, n_loaded_seqs = len(loaded_seqs[0]), len(loaded_seqs)

print(f"The loaded MSA has {n_loaded_seqs} sequences and {n_loaded_pos} \
      positions.")

The loaded MSA has 1390 sequences and 832       positions.

MSA filtering

We clean the loaded MSA by filtering both sequences and positions.

sequences, sequences_id, positions = c_msa.filter_sequences(
    loaded_seqs, loaded_seqs_id, gap_threshold=0.4, seq_threshold=0.2)
n_pos = len(positions)
print(f"After filtering, we have {n_pos} remaining positions.")
print(f"After filtering, we have {len(sequences)} remaining sequences.")

After filtering, we have 243 remaining positions.
After filtering, we have 1376 remaining sequences.

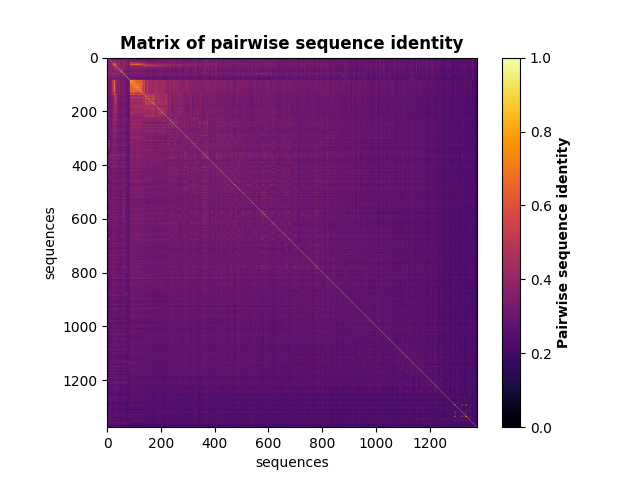
Compute the matrix of pairwise sequence identity

Note that the sequences in the matrix are in the same order as in the MSA. You can use cocoatree.visualization.update_tree_ete3_and_return_style() function to represent a sequence similarity matrix ordered following a phylogenetic tree (see Plot XCoR together with (phylogenetic) tree and metadata).

identity_matrix = c_msa.compute_seq_identity(sequences)

fig, ax = plt.subplots()
m = ax.imshow(identity_matrix, vmin=0, vmax=1, cmap='GnBu')
ax.set_xlabel("sequences", fontsize=10)
ax.set_ylabel("sequences", fontsize=10)
ax.set_title('Matrix of pairwise sequence identity', fontweight="bold")
cb = fig.colorbar(m)
cb.set_label("Pairwise sequence identity", fontweight="bold")

Compute sequence weights

seq_weights, m_eff = c_msa.compute_seq_weights(sequences)
print('Number of effective sequences %d' %
      np.round(m_eff))

Number of effective sequences 1019

Compute conservation along the MSA

Di = c_pos.compute_conservation(sequences, seq_weights)

fig, ax = plt.subplots(figsize=(9, 4))
xvals = [i+1 for i in range(len(Di))]
xticks = [0, 50, 100, 150, 200, 250]
ax.bar(xvals, Di, color='k')
plt.tick_params(labelsize=11)
ax.set_xticks(xticks)
ax.set_xlabel('residues', fontsize=14)
ax.set_ylabel('Di', fontsize=14)

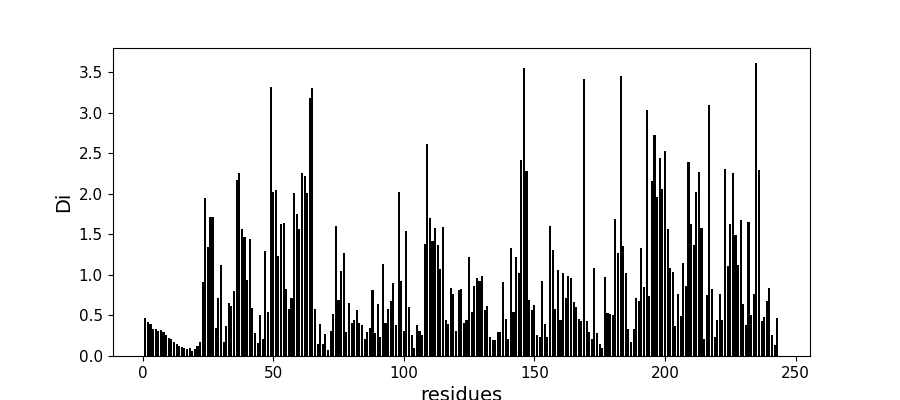
Text(72.97222222222221, 0.5, 'Di')

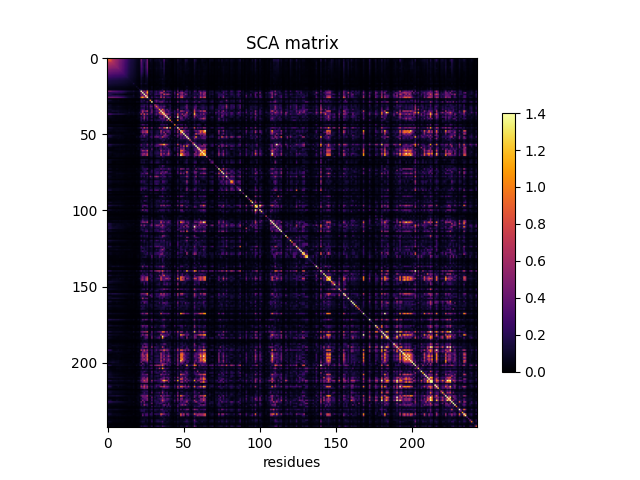
Compute the SCA coevolution matrix

SCA_matrix = c_pw.compute_sca_matrix(sequences, seq_weights)

fig, ax = plt.subplots()
im = ax.imshow(SCA_matrix, vmin=0, vmax=1.4, cmap='inferno')

ax.set_xlabel('residues', fontsize=10)
ax.set_ylabel(None)
ax.set_title('SCA matrix')
fig.colorbar(im, shrink=0.7)

<matplotlib.colorbar.Colorbar object at 0x7f5e7188e2d0>

Extract principal components (PCA analysis) and independent components (ICA analysis) ———————————————————————-

(this can take some time because of randomization)

n_components = 9
principal_components = c_deconv.extract_principal_components(
    SCA_matrix)
idpt_components = c_deconv.extract_independent_components(
    SCA_matrix,
    n_components=n_components)

Plot components

n_components_to_plot = n_components
if n_components_to_plot % 2:
    print('Odd number of components: the last one is discarded for \
          visualization')
    n_components_to_plot -= 1

pairs = [[x, x+1] for x in range(0, n_components_to_plot, 2)]
ncols = len(pairs)
plt.rcParams['figure.figsize'] = 14, 8
fig, axes = plt.subplots(nrows=2, ncols=len(pairs), tight_layout=True)
for k, [k1, k2] in enumerate(pairs):
    ax = axes[0, k]
    ax.plot(principal_components[k1], principal_components[k2], 'ok')
    ax.set_xlabel("PC %i" % (k1+1), fontsize=16)
    ax.set_ylabel("PC %i" % (k2+1), fontsize=16)

    ax = axes[1, k]
    ax.plot(idpt_components[k1], idpt_components[k2], 'ok')
    ax.set_xlabel("IC %i" % (k1+1), fontsize=16)
    ax.set_ylabel("IC %i" % (k2+1), fontsize=16)

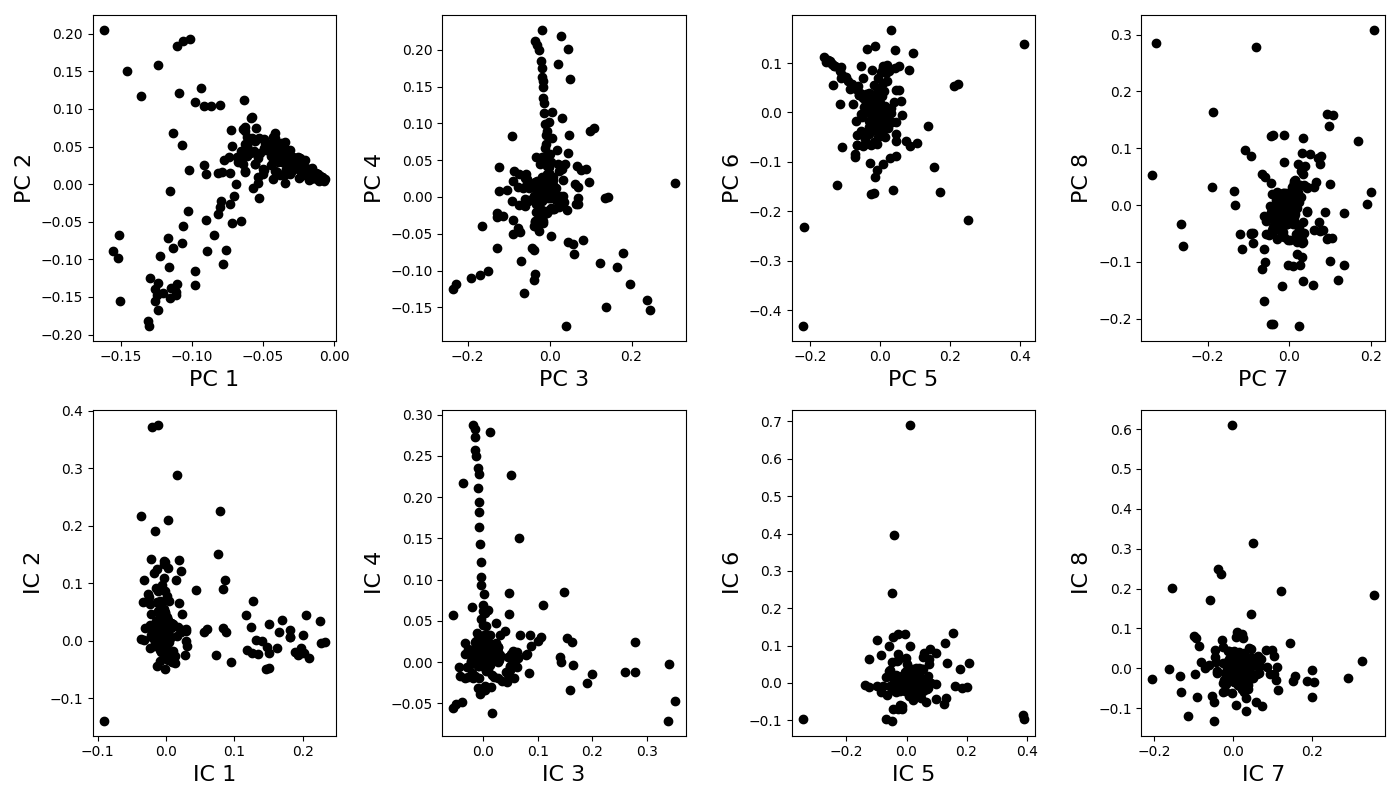
Odd number of components: the last one is discarded for           visualization

Extract XCoRs

Obtain a list of residues of each XCoR

xcors = c_deconv.extract_xcors_from_ICs(idpt_components, SCA_matrix)

print('XCoR positions on (filtered) sequences:')
for isec, sec in enumerate(xcors):
    print('XCoR %d: %s' % (isec+1, sec))

XCoR positions on (filtered) sequences:
XCoR 1: [64, 48, 145, 195, 63, 182, 199, 168, 146, 197, 144, 108, 222, 61, 196, 198, 194, 211, 49, 216, 208, 192, 234, 26, 35, 62, 235, 50, 155, 200, 23, 60, 76, 213, 73, 58, 114, 25]
XCoR 2: [140, 202, 52, 110, 78, 87, 81, 129, 75, 124, 33, 32, 128, 82, 207, 226, 120, 83, 69, 31]
XCoR 3: [225, 190, 212, 223, 180, 183, 184, 220, 224, 193, 172, 210, 142, 176, 160, 177, 217, 219, 161, 227]
XCoR 4: [0, 1, 2, 3, 4, 5, 6, 22, 7, 8, 9, 10, 11, 12, 13, 158, 14]
XCoR 5: [24, 228, 51, 215, 188]
XCoR 6: [97, 100, 98, 101, 95, 91, 107, 126, 102]
XCoR 7: [231, 109, 59, 53, 206, 131, 130]
XCoR 8: [57, 36, 111, 204, 34, 117]
XCoR 9: [46, 39, 37, 38, 156, 152, 41, 201, 149, 148, 143]

Note that the residue positions do not follow the order of the sequence but are ordered following a decreasing contribution to the independent component (the first residue of the list has the highest score).

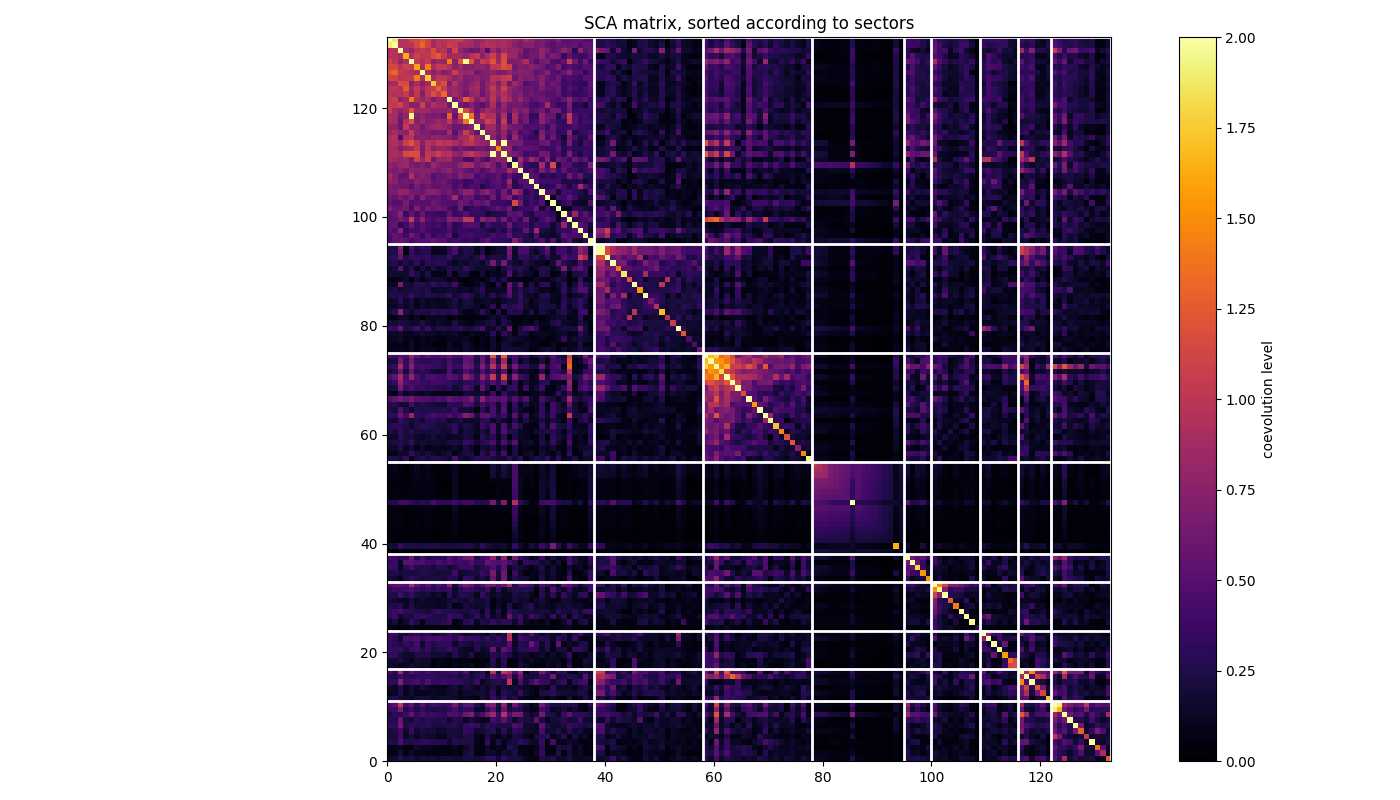
Plot coevolution within and between the XCoRs

Each white square corresponds to a XCoR, with the residues ordered in decreasing contribution to the independent component associated from top to bottom and from left to right.

fig, ax = plt.subplots(tight_layout=True)

xcor_sizes = [len(sec) for sec in xcors]
cumul_sizes = sum(xcor_sizes)
sorted_pos = [s for sec in xcors for s in sec]

im = ax.imshow(SCA_matrix[np.ix_(sorted_pos, sorted_pos)],
               vmin=0, vmax=2,
               interpolation='none', aspect='equal',
               extent=[0, cumul_sizes, 0, cumul_sizes], cmap='inferno')
ax.set_title('SCA matrix, sorted according to XCoRs')
cb = fig.colorbar(im)
cb.set_label("coevolution level")

line_index = 0
for i in range(n_components):
    ax.plot([line_index + xcor_sizes[i], line_index + xcor_sizes[i]],
            [0, cumul_sizes], 'w', linewidth=2)
    ax.plot([0, cumul_sizes], [cumul_sizes - line_index,
                               cumul_sizes - line_index], 'w', linewidth=2)
    line_index += xcor_sizes[i]

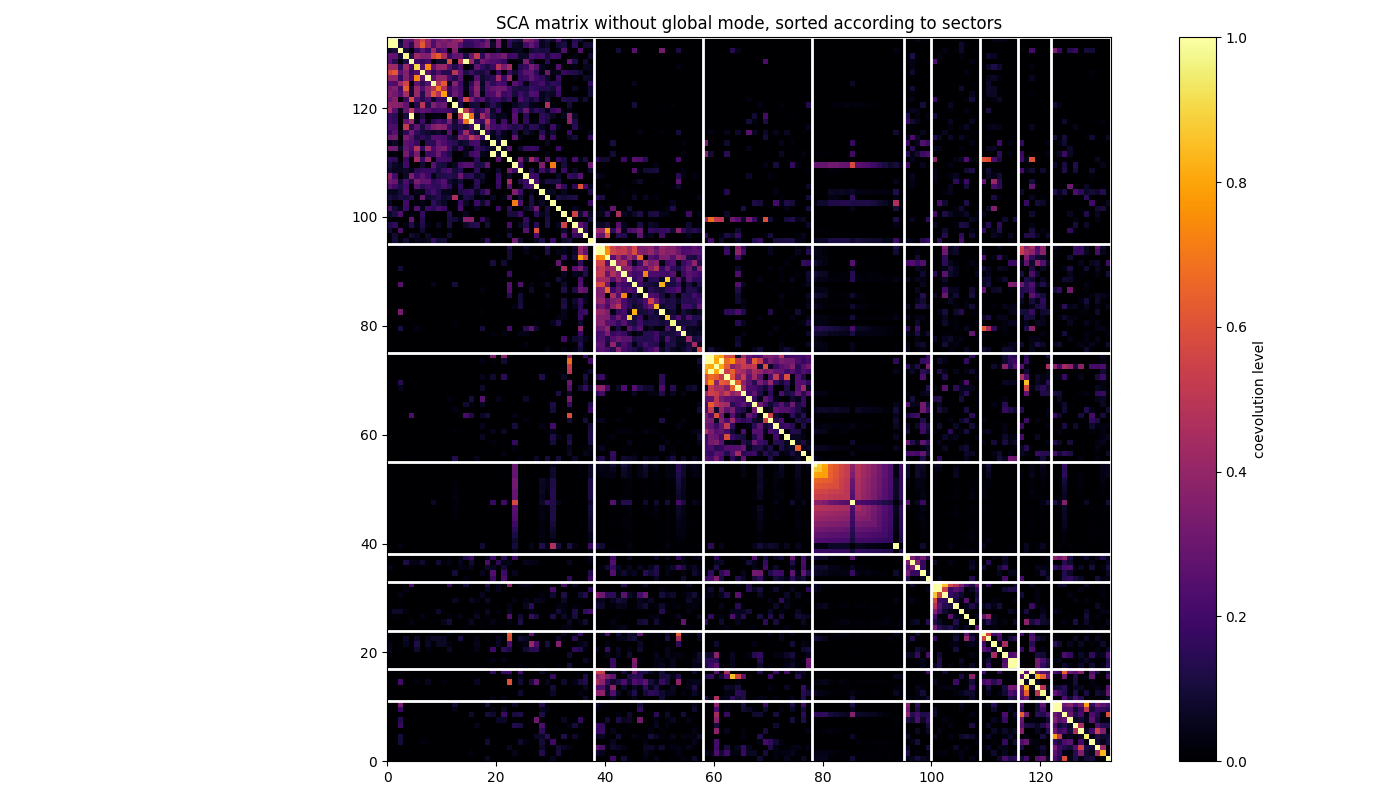
Do the same but for the SCA matrix where a global correlation mode has been removed and, hence, such that XCoRs are better highlighted. See Rivoire et al., PLOSCB, 2016

# Removing a global mode (ngm = no global mode),
# i.e., setting largest eigeinvalue to zero
SCA_matrix_ngm = c_deconv.remove_global_correlations(SCA_matrix)

# plotting
fig, ax = plt.subplots(tight_layout=True)
im = ax.imshow(SCA_matrix_ngm[np.ix_(sorted_pos, sorted_pos)], vmin=0, vmax=1,
               interpolation='none', aspect='equal',
               extent=[0, sum(xcor_sizes), 0, sum(xcor_sizes)],
               cmap='inferno')
ax.set_title('SCA matrix without global mode, sorted according to XCoRs')
cb = fig.colorbar(im)
cb.set_label("coevolution level")

line_index = 0
for i in range(n_components):
    ax.plot([line_index + xcor_sizes[i], line_index + xcor_sizes[i]],
            [0, sum(xcor_sizes)], 'w', linewidth=2)
    ax.plot([0, sum(xcor_sizes)], [sum(xcor_sizes) - line_index,
                                   sum(xcor_sizes) - line_index],
            'w', linewidth=2)
    line_index += xcor_sizes[i]

Export XCoR sequences in fasta format

The file can then be used for visualization along a phylogenetic tree as implemented in cocoatree.visualization.

Here, the positions are ordered in decreasing contribution to the independent component to which the XCoR is associated.

xcor_1_pos = list(positions[xcors[0]])
xcor_1 = []
for sequence in range(len(sequences_id)):
    seq = ''
    for pos in xcor_1_pos:
        seq += loaded_seqs[sequence][pos]
    xcor_1.append(seq)

c_io.export_fasta(xcor_1, sequences_id, 'xcor_1.fasta')

if False:  # need to be revised
    # %
    # Export files necessary for Pymol visualization
    # Load PDB file of rat's trypsin
    pdb_seq, pdb_pos = c_io.load_pdb('data/3TGI.pdb', pdb_id='TRYPSIN',
                                     chain='E')
    # Map PDB positions on the MSA sequence corresponding to rat's trypsin:
    # seq_id='14719441'
    pdb_mapping = c_msa.map_to_pdb(pdb_seq, pdb_pos, sequences, sequences_id,
                                   pdb_seq_id='14719441')
    # Export lists of the first XCoR positions and each residue's
    # contribution to the independent component to use for visualization on
    # Pymol.
    # The residues are ordered in the list by decreasing contribution score
    # (the first residue in the list is the highest contributing)
    c_io.export_xcor_for_pymol(pdb_mapping, idpt_components.T, axis=0,
                               xcor_pos=xcor_1_pos,
                               ics=xcors,
                               outpath='color_xcor_1_pymol.npy')